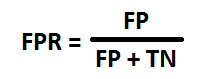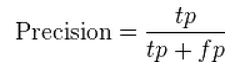[edit 2014/04/19: Some mistakes were made, but the interpretation follows. Sorry about that.]

TL;DR

Use Precision Recall area under curve for class imbalance problems. If not, Receiver Operating Characteristic area under curve otherwise.

Introduction

When being confronted with the class imbalance problem, accuracy is a wrong metric to use. Usually, there are two candidates as metrics:

Receiver Operating Characteristic area under curve (ROC AUC)
Precision Recall area under curve (PR AUC)

Which is better? What are the differences?

Receiver Operating Characteristic Curve (ROC curve)

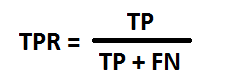
A ROC curve is plotting True Positive Rate (TPR) against False Positive Rate (FPR).

TPR is defined as:

FPR is defined as:

where TP = true positive, TN = true negative, FP = false positive, FN = false negative.

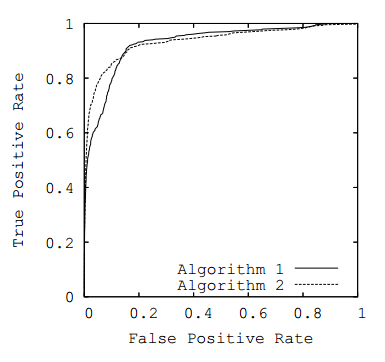
A typical ROC curve looks like this, which shows two ROC curves for Algorithm 1 and Algorithm 2.

The goal is to have a model be at the upper left corner, which is basically getting no false positives – a perfect classifier.

The receiver operating characteristic area under curve (ROC AUC) is just the area under the ROC curve. The higher it is, the better the model is.

Precision Recall Curve (PR Curve)

A PR curve is plotting Precision against Recall.

Precision is defined as:

Recall is defined as:

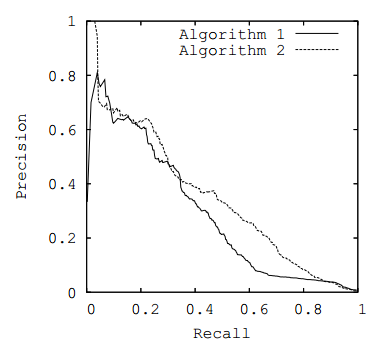
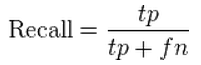A typical PR curve looks like this, which shows two PR curves for Algorithm 1 and Algorithm 2.

The goal is to have a model be at the upper right corner, which is basically getting only the true positives with no false positives and no false negatives – a perfect classifier.

The precision recall area under curve (PR AUC) is just the area under the PR curve. The higher it is, the better the model is.

Differences between the ROC AUC and PR AUC

Randy has given a great explanation here, plus a little of my understanding.

Since PR does not account for true negatives (as TN is not a component of either Precision or Recall), or there are many more negatives than positives (a characteristic of class imbalance problem), use PR. If not, use ROC.

A small example from Randy to illustrate this more clearly, with some bold text added myself:

For illustration, let’s take an example of an information retrieval problem where we want to find a set of, say, 100 relevant documents out of a list of 1 million possibilities based on some query. Let’s say we’ve got two algorithms we want to compare with the following performance:

Method 1: 100 retrieved documents, 90 relevant. Thus, TP = 90, TN = 999890, FP = 10, FN = 10.

Method 2: 2000 retrieved documents, 90 relevant. Thus, TP = 90, TN = 997990, FP = 1910, FN = 10.

Clearly, Method 1’s result is preferable since they both come back with the same number of relevant results, but Method 2 brings a ton of false positives with it. The ROC measures of TPR and FPR will reflect that, but since the number of irrelevant documents dwarfs the number of relevant ones, the difference is mostly lost:

Method 1: 0.9 TPR, 0.00001 FPR

TPR = TP/(TP + FN) = 90/(90 + 10) = 0.9

FPR = FP/(FP + TN) = 10/(10 + 999890) = 0.00001

Method 2: 0.9 TPR, 0.00191 FPR (difference of 0.0019)

TPR = TP/(TP + FN) = 90/(90 + 10) = 0.9

FPR = FP/(FP + TN) = 1910/(1910 + 997990) = 0.0019

Precision and recall, however, don’t consider true negatives and thus won’t be affected by the relative imbalance (which is precisely why they’re used for these types of problems):

Method 1: 0.9 precision, 0.9 recall

Precision = TP/(TP + FP) = 90/(90 + 10) = 0.9

Recall = TP/(TP + FN) = 90/(90 + 10) = 0.9

~~Method 2: 0.9 precision, 0.045 recall (difference of 0.855) <= Randy’s post made a mistake here.~~

Method 2: 0.045 precision (difference of 0.855), 0.9 recall

Precision = TP/(TP + FP) = 90/(90 + 1910) = 0.045

Recall = TP/(TP + FN) = 90/(90 + 10) = 0.9

Obviously, those are just single points in ROC and PR space, but if these differences persist across various scoring thresholds, using ROC AUC, we’d see a very small difference between the two algorithms, whereas PR AUC would show quite a large difference.

To compare both methods, using ROC_AUC, we see that the FPR has a difference of 0.0019, which is very small. However, using PR_AUC, we see that the Precision has a difference of 0.855 which is much more pronounced.

Clearly, the PR is much better in illustrating the differences of the algorithms in the case where there are a lot more negative examples than the positive examples.

Conclusion

Use PR AUC for cases where the class imbalance problem occurs, otherwise use ROC AUC.

One note though, if your problem set is small (thus having fewer points in PR curve), the PR AUC metric could be over-optimistic because AUC is calculated via the trapezoid rule, but linear interpolation on the PR curve does not work very well, which the PR curve example above looks very wiggly. Interested readers may consult this paper of The Relationship between Precision-Recall and ROC Curves. Though, practically in a class imbalance problem nowadays, you should have a lot of examples so this should not be a problem.